线面垂直是几何学中的基本概念，它在空间几何、立体几何以及数学的其他分支中都有着广泛的应用，对于初学者来说，理解和掌握线面垂直的概念和性质是非常重要的，本文将围绕线面垂直的概念、性质、判定方法以及应用展开讲解，帮助读者更好地理解和掌握线面垂直的相关知识。

线面垂直的基本概念

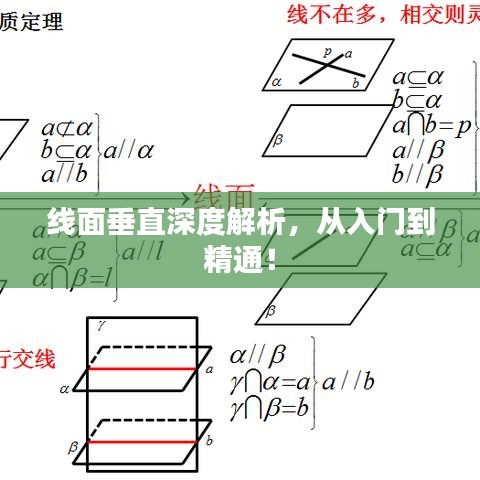
线面垂直，就是一条直线与一个平面之间的关系，当这条直线与平面内的任意一条直线都垂直时，我们就说这条直线与这个平面垂直，这个概念是几何学中的基础概念之一，对于理解空间几何和立体几何非常重要。

线面垂直的性质

线面垂直具有以下几个重要的性质：

1、若一条直线垂直于一个平面，则这条直线与平面内的所有直线都垂直。

2、若两条直线垂直于同一个平面，则这两条直线之间的夹角为直角。

3、若一个平面内的两条直线都垂直于另一条直线，则这条直线垂直于这个平面。

线面垂直的判定方法

判定线面垂直的方法主要有以下几种：

1、若直线与平面内的一条直线平行且都与另一条不平行于平面的直线垂直，则这条直线垂直于这个平面。

2、若直线与平面内两条不同的直线都垂直，则这条直线垂直于这个平面。

3、若直线的方向向量与平面的法向量平行，则这条直线垂直于这个平面，这是从向量角度判定线面垂直的方法。

线面垂直的应用

线面垂直在生活和工作中有着广泛的应用，例如在建筑、机械、计算机图形学等领域，在建筑设计中，线面垂直的概念被用来描述建筑物的结构和形状；在机械工程中，线面垂直的概念被用来描述机械零件之间的关系；在计算机图形学中，线面垂直的概念被用来绘制三维图形等。

线面垂直的实例解析

为了更好地理解线面垂直的概念和应用，我们可以通过一些实例来解析，我们可以观察教室中的墙壁和地面，地面与墙壁的交线可以看作是一条直线，而墙壁可以看作是一个平面，当这条直线与墙面垂直时，它就与墙面所在的平面垂直，这就是一个典型的线面垂直的例子，通过对这个例子的分析，我们可以更直观地理解线面垂直的概念和性质。

本文围绕线面垂直的概念、性质、判定方法以及应用进行了详细的讲解，通过本文的学习，读者应该能够理解和掌握线面垂直的基本概念、性质以及判定方法，并能够理解其在生活和工作中的应用，希望本文能够帮助读者更好地理解和掌握线面垂直的相关知识。